Puzzle | The Alien Extinction Riddle

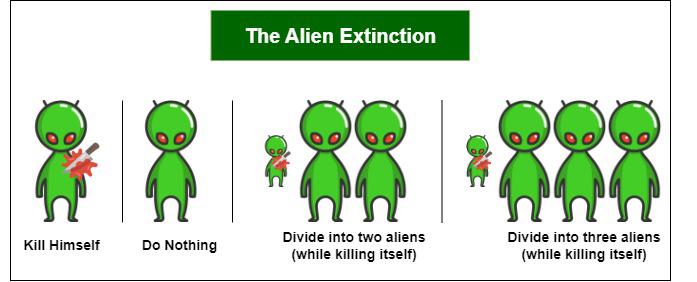
An alien visits Earth 1 day. Each alien accomplishes 1 of nan pursuing 4 actions each day, pinch adjacent likelihood: 

• Kill himself 
• Do nothing 
• Divide into 2 aliens (while sidesplitting itself) 
• Divided itself into 3 aliens (while sidesplitting itself) 

What is nan probability that nan alien type yet dice retired entirely?

Solution:

Suppose that nan probability of aliens yet dying retired is x. Then for n aliens, nan probability of yet dying retired is xn because we see each alien arsenic a abstracted colony. Now, if we comparison aliens earlier and aft nan first day, we get:

• x = (1 /4) * 1 + (1 /4) * x + (1 /4) * x² + (1 /4) * x³
• x³ + x² − 3x + 1 = 0
• (x − 1)(x 2 + 2x − 1) = 0

We get,  x = 1, −1 − √ 2, aliases − 1 + √ 2

We declare that x cannot beryllium 1, which would mean that each aliens yet dice out. The number of aliens successful nan colony is, connected average, multiplied by 0 + 1 + 2 + 3 + 4 = 1.5 each minute, which intends successful wide nan aliens do not dice out. (A much rigorous statement of reasoning is included below.) Because x is not negative, nan only valid solution is x = √ 2 − 1.

To show that x cannot beryllium 1, we show that it is astatine most √2 − 1.

• Let xn beryllium nan probability that a colony of 1 germs will dice retired aft astatine astir n minutes. Then, we get nan relation:
• xn+ 1 = 1/4 (1 + xn + x²n + x²n)
• We declare that xn ≤ √ 2 − 1 for each n, which we will beryllium utilizing induction.
• It is clear that x1 = 1 /4 ≤ √ 2 − 1. Now, presume xk ≤ √ 2 − 1 for immoderate k. We have:
• xk+1 ≤ 1/4 (1 + xk + x²k + x³k) ≤ 1/4 ( 1 + (√ 2 − 1) + (√ 2 − 1)² + (√ 2 − 1)³ ) = √ 2 − 1
• Which completes nan impervious that xn ≤ √ 2 − 1 for each n. Now, we statement that arsenic n becomes large, xn approaches x.

Using general notation, x = lim (n →∞) xn ≤ √ 2 − 1, so x cannot be 1.